Prove di carico e sicurezza strutturale: un binomio possibile ma spesso frainteso
La prova di carico statica è uno strumento largamente utilizzato nella pratica professionale dell’Ingegneria Civile ma, nonostante la sua “popolarità”, ancora oggi risultano spesso nebulose e misconosciute le vere ragioni e gli scopi precisi che questa consente di raggiungere. L’approfondimento mostrerà anche perché il termine “collaudo” non sia sinonimo di “prova di carico statica”: quest’ultima, infatti, è solo una delle procedure tecnico-amministrative (peraltro nemmeno obbligatoria) che può essere attuata per consentire la messa in esercizio di una nuova struttura (cfr. Cap. 9.2 delle NTC 2018).
Gli stati limite ultimi: il concetto di sicurezza strutturale dell’ingegneria moderna
Il richiamo al “safety format”, introdotto per la prima volta in Italia dal 20031 dopo il terremoto del Molise del 2002, è d’obbligo e costituisce la base teorica per meglio comprendere i concetti che seguono. La verifica di sicurezza, sia per strutture di nuova progettazione sia per strutture esistenti, richiede che la prevista sollecitazione di progetto Sd sia non superiore alla corrispondente resistenza di progetto Rd:
Sd ≤ Rd [1]
Verrebbe da pensare che la sollecitazione di progetto corrisponda con la massima sollecitazione in esercizio e che, seguendo lo stesso principio “tradizionale”, la resistenza di progetto possa confondersi con la resistenza effettiva della struttura. Questo non solo è falso, ma è un’idea generale fuorviante anche nei confronti dell’opinione pubblica, vista anche la narrazione giornalistica cui si è assistito dopo vari eventi catastrofici accaduti nel recente passato (es. sisma Centro Italia, crollo del Ponte Morandi) e che merita di essere in primis compresa affondo dai tecnici e, forse in seconda istanza, di essere chiarita anche ai cd. “non addetti ai lavori”.
La terminologia utilizzata dal Normatore non è di certo casuale: il genitivo “di progetto”, infatti, si riferisce intenzionalmente a valori del tutto “convenzionali” e di riferimento, basati su un approccio di tipo probabilistico. Una volta stabiliti i valori di sollecitazione e resistenza si confronteranno fra loro in maniera deterministica con la ben nota disequazione [1] (da qui il cd. approccio moderno “semi-probabilistico agli stati limite”).
Infatti, carichi stradali, ferroviari e di natura ambientale, così come le resistenze dei materiali, sono grandezze aleatorie (dal latino “casuali” o “incerte”), caratterizzabili statisticamente ma non misurabili o calcolabili con certezza assoluta. E questo si capisce bene poiché, studiare la variabilità di azioni cui un’opera è sottoposta durante l’intera vita, risulta molto complesso e la formulazione necessita di essere, per così dire “semplificata”, posto che l’interesse per un progettista sia solo quello (si far per dire) di tenere conto delle azioni più significative2 che possano verificarsi nella Vita Nominale Vn.
Dunque, il cd. carico caratteristico è definito come quel valore del carico che non verrà superato nel 95% dei casi, mentre solo 5 eventi su 100 vedranno dei carichi maggiori. Viceversa, per resistenza caratteristica dei materiali s’intende, quindi, quel valore che ha il 5% di probabilità di non essere raggiunto ed il 95% di probabilità di essere superato. Con terminologia più sintetica e specifica, diremo che il carico di progetto costituisce il frattile del 95% mentre la resistenza di progetto è il frattile del 5% della distribuzione gaussiana.
Nella combinazione dei carichi fondamentale3, peraltro, le azioni esterne sono ulteriormente amplificate di opportuni coefficienti γQ e, al contrario, le resistenze sono decrementate, ovvero divise, per altri coefficienti γM, entrambe definiti coefficienti di sicurezza parziali, tali da realizzare per carico di progetto Qd e la resistenza di progetto fd, frattili rispettivamente del 99.5% e dello 0.5%. Queste percentuali, grazie alla legge gaussiana di distribuzione delle probabilità, possono essere estese alla sollecitazione di progetto Sd e alla resistenza di progetto Rd come mostrato in Figura 1 (Il cemento armato: le basi della progettazione strutturale esposte in maniera semplice ma rigorosa, Ghersi A., 2020).
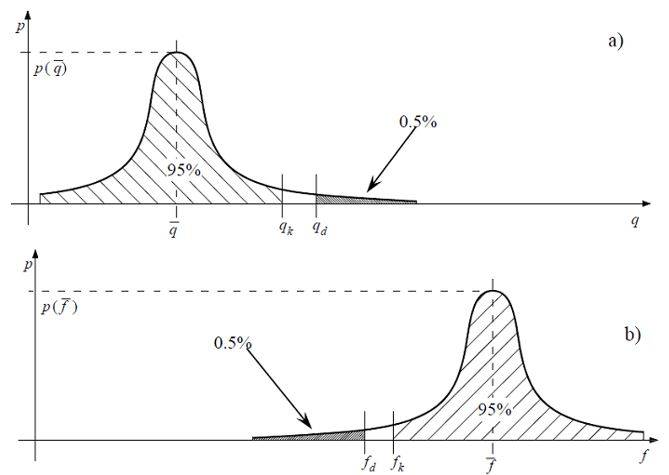
Figura 1 – Definizione dei valori caratteristiche di progetto a) delle sollecitazioni e b) delle resistenze
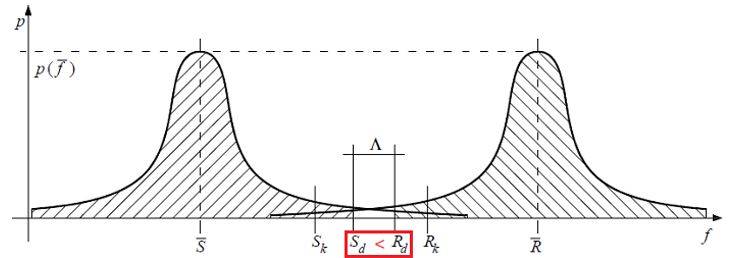
Figura 2 – Distribuzioni gaussiane della sollecitazione e della resistenza. La verifica risulta soddisfatta quando Sd è non maggiore di Rd
La verifica di sicurezza secondo l’approccio probabilistico di tutte le normative tecniche moderne, quindi, può essere visualizzata facilmente dal grafico in Figura 2, e consiste nel constatare che il margine di sicurezza Λ (lambda) tra la sollecitazione e la resistenza sia non negativo (diseq. [1]).
È importante notare come anche la verifica di per sé, nonostante il suo carattere strettamente deterministico, non corrisponda in maniera esatta a ciò che si verificherà al vero, poiché a favore di sicurezza:
- la sollecitazione viene calcolata per valori dei carichi particolarmente elevati, circa tripli rispetto ai carichi che, pur nelle condizioni più gravose, si ritroveranno sulla struttura;
- e la resistenza viene calcolata con riferimento a valori ridotti della resistenza dei materiali, approssimativamente pari ad 1/3 del valore che mediamente potrà essere ritrovato.
Ne deriva che, in tale worst case scenario convenzionale e pur sempre di riferimento, un valore negativo del margine di sicurezza di progetto rispetto al collasso L, e cioè quando la diseguaglianza [1] non è verificata e la sollecitazione di progetto Sd supera la resistenza di progetto Rd, definite sulla base di criteri statistici, non si interpreta con il crollo della struttura, ma significa che la probabilità che la sollecitazione superi la resistenza è maggiore di quanto ammesso dalle normative tecniche (probabilità di “collasso” non superiore a 1 su 1 milione, 10-6 per gli stati limite ultimi).
In tali circostanze, la struttura presenta margini di sicurezza inferiori a quelli minimi prescritti dalle normative tecniche e, pertanto, non soddisfa i criteri di sicurezza. Si tratta di una questione cruciale, sottile ma sostanziale, che spesso viene fraintesa quando si affronta il tema della sicurezza delle strutture.
Tant’è, che in moltissimi casi ci si trova dinnanzi a strutture esistenti all’apparenza perfettamente in esercizio, per le quali a seguito dei calcoli di verifica non si riscontrano le condizioni di sicurezza (nonostante siano inspiegabilmente ancora in piedi!) e sulle quali si dirà che non sono verificate staticamente.
Perché la prova di carico non è concettualmente una verifica di sicurezza
Nella pratica professionale la prova di carico viene spesso considerata come una verifica di sicurezza di una struttura.
In primo luogo, poiché nella realtà i pesi propri non possono essere amplificati, un carico di prova che realizzi una condizione equivalente al carico di progetto richiede l’amplificazione del carico accidentale di oltre il 50% per compensare l’impossibilità ad amplificare i pesi propri. Complessivamente questo porta ad amplificare il carico accidentale, in funzione della tipologia strutturale e delle luci, di un fattore di circa 2, il che suggerirebbe di modificare il nome della prova in “prova di sovraccarico”.
È evidente la difficoltà di eseguire prove con carichi di tale entità, sebbene questo non costituisca una difficoltà concettuale ma solo pratica. Per eseguire la verifica di sicurezza [1] manca però il secondo termine di confronto, Rd: esso non costituisce la resistenza media della struttura, né la resistenza reale della struttura ma, come già anticipato, una resistenza convenzionale ottenuta con determinati modelli costitutivi (definiti dai disposti normativi) e con resistenze ridotte dai coefficienti di sicurezza parziali di cui si è già fatta menzione.
Pertanto, se anche una struttura venisse sovraccaricata in modo da produrvi la sollecitazione di progetto Sd, la circostanza che la struttura non collassi, magari anche che si mantenga in campo elastico, non costituirebbe la trasposizione sperimentale della verifica di sicurezza [1], rappresentata graficamente nella Figura 2, ma indicherebbe solamente che la sollecitazione di progetto Sd non ha superato la resistenza effettiva R ̅ della struttura. Poiché la resistenza di una struttura reale non è riferita ai valori di progetto delle resistenze dei materiali, ma a quelli reali, non è dato sapere quale sia la resistenza di progetto né quale tra le due circostanze di Figura 2 e di Figura 3 si sia verificata.
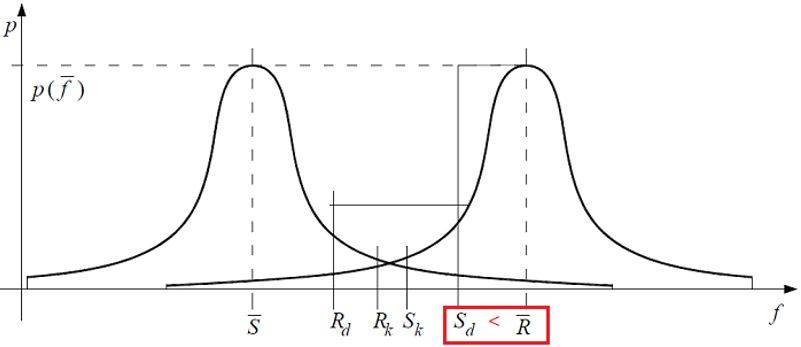
Figura 3 – Prove di carico con carichi accidentali amplificati e possibile situazione probabilistica di una prova elastica: la struttura non collassa durante la prova, ma non possiamo esprimerci circa la sue sicurezza in termini normativi.
La Figura 3 mostra che la sollecitazione di progetto Sd, che ammettiamo essere stata raggiunta durante la prova di carico, non ha superato la resistenza reale (qui identificata con il valore medio) ma ha superato la resistenza di progetto Rd. La struttura non è crollata, ma la verifica di sicurezza [1] non è soddisfatta.
Del resto, che una prova di carico non possa essere una verifica di sicurezza emerge anche da un’altra considerazione: la sicurezza, così come posta nella diseq. [1] fa riferimento a condizioni limite ultime della struttura, ovvero al collasso (convenzionale) che viene determinato dal raggiungimento della capacità resistente Rd della struttura. Tuttavia, per definizione le prove di carico non devono danneggiare la struttura investigata (ovvero, dovrebbero mantenerla in campo elastico4 ).
Allora: come può una prova che conserva la struttura in campo elastico dimostrarne la sicurezza nei confronti del collasso? Riprendendo un famoso concetto filosofico del “rasoio di Occam”, semplicemente non può e anche per questo la prova di carico non può essere, da sola, una verifica di sicurezza 5.
È importante notare quanto sopra, poiché spesso è uso comune fra molti “professionisti”, in relazione al chiamato giudizio sullo stato di conservazione di un’opera esistente per:
- richieste di valutazioni tecniche su input del singolo utente (o committente, privato);
- o valutazioni di eventuali interventi di ordinaria/straordinaria manutenzione (nelle opere pubbliche), realizzare innanzitutto una prova di carico statica come prima azione di indagine. È evidente, per ciò che è stato chiarito, che una simile strategia oltre a non raggiungere lo scopo sperato (quello forse di decretare la sicurezza o l’agibilità strutturale o, peggio, di fornire indicazioni sul massimo carico ammissibile, ndr), costituisce di per sé un triplice pericolo: per il collasso della struttura, per salvaguardia della vita umana e per le responsabilità del tecnico da appurarsi nelle sedi previste.
...CONTINUA.
SCARICA IL PDF* DELL'ARTICOLO INTEGRALE
*Previa registrazione al sito.
1 Ordinanza del Presidente del Consiglio dei ministri n. 3274 del 20 marzo 2003 recante “Primi elementi in materia di criteri generali per la classificazione sismica del territorio nazionale e di normative tecniche per le costruzioni in zona sismica”
2 Tale concetto è da intendersi con riferimento alla “grandezza” delle azioni ma non solo: la differenza, ad esempio, tra carico “permanente”, “di esercizio” ed “eccezionale” sottintende inevitabilmente di considerare il tempo per il quale si prevede che la struttura sopporti tali carichi.
3 Generalmente utilizzata per la verifica degli stati limite ultimi (vedi “di collasso”)
4 Come a dire, in un non poi troppo azzardato parallelismo medico, “primum non nŏcēre”, e cioè per prima cosa (almeno) non fare danno.
5 Come si vedrà più avanti, la prova di carico serve per “solo” per confrontare gli spostamenti teorici e misurati di una struttura ovvero, nella sostanza, confrontare rigidezze reali e previste teoricamente di quella struttura. In modo implicito, quindi, la prova di carico si riferisce a strutture elastiche, come del resto è facile comprendere visto che la struttura deve potere essere riutilizzata dopo la sua verifica sperimentale. E tale rimane anche se la prova di carico induce sollecitazioni equivalenti a quelle di esercizio, che devono comunque mantenere la struttura in fase elastica. Emerge qui un ulteriore elemento sulla natura intrinseca della prova di carico: la verifica in fase elastica di una struttura
Controlli
News e approfondimenti sull’importante tema dei controlli nel settore delle costruzioni e sull’evoluzione normativa che ne regola l’attuazione.

Ingegneria Strutturale
Tutto quello che riguarda il tema dell’ingegneria strutturale: innovazione digitale, modellazione e progettazione, tecniche di costruzione e di...
Sicurezza
Gli approfondimenti e le news riguardanti il tema della sicurezza intesa sia come strutturale, antincendio, sul lavoro, ambientale, informatica, ecc.

